Geometrické vzorce pro trojúhelníky a čtyřúhelníky

U pravoúhlého trojúhelníku si pamatuj hlavně Pythagorovu větu: c² = a² + b², kde c je přepona (strana naproti pravému úhlu) a a, b jsou odvěsny. Z téhle rovnice si můžeš vyjádřit i jednotlivé strany, když znáš ty ostatní.

Pro obecný trojúhelník se hodí znát vzorec pro obsah S = $a · v_a$/2, kde a je strana a v_a je výška na tu stranu. Obvod trojúhelníku je jednoduchý - prostě sečteš všechny strany: o = a + b + c.

💡 Když počítáš obsah trojúhelníku, vždycky si můžeš vybrat, kterou stranu použiješ jako základnu a pak k ní hledat příslušnou výšku!

U čtyřúhelníků jsou nejdůležitější vzorce pro čtverec a obdélník. Čtverec má obvod o = 4 · a a obsah S = a². Nezapomeň, že obsah čtverce můžeš spočítat i pomocí úhlopříčky: S = u²/2. Pro obdélník platí o = 2 · $a + b$ a obsah S = a · b, kde a a b jsou jeho strany.

Další čtyřúhelníky a kruhové útvary

Kosočtverec má obvod o = 4 · a a obsah S = a · v_a, kde v_a je výška. Obsah můžeš spočítat i pomocí úhlopříček: S = (u₁ · u₂)/2. Pro kosodélník platí o = 2 · $a + b$ a obsah S = a · v_a = b · v_b.

Lichoběžník má dvě rovnoběžné základny a a c, ramena b a d, a výšku v. Jeho obvod je o = a + b + c + d a obsah S = $(a + c) · v$/2 - průměr základen krát výška děleno dvěma.

U kruhu si pamatuj, že r je poloměr a d = 2r je průměr. Obvod kruhu je o = 2πr a obsah S = πr². Hodnota π je přibližně 3,14.

🔍 Pozor na jednotky! Když máš délky v cm, vyjde ti obsah v cm² a objem v cm³.

Rotační válec má obsah podstavy S_p = πr² a obsah pláště S_pl = 2πrv, kde v je výška. Celkový povrch je S = 2S_p + S_pl a objem V = S_p · v = πr² · v.

Tělesa v prostoru

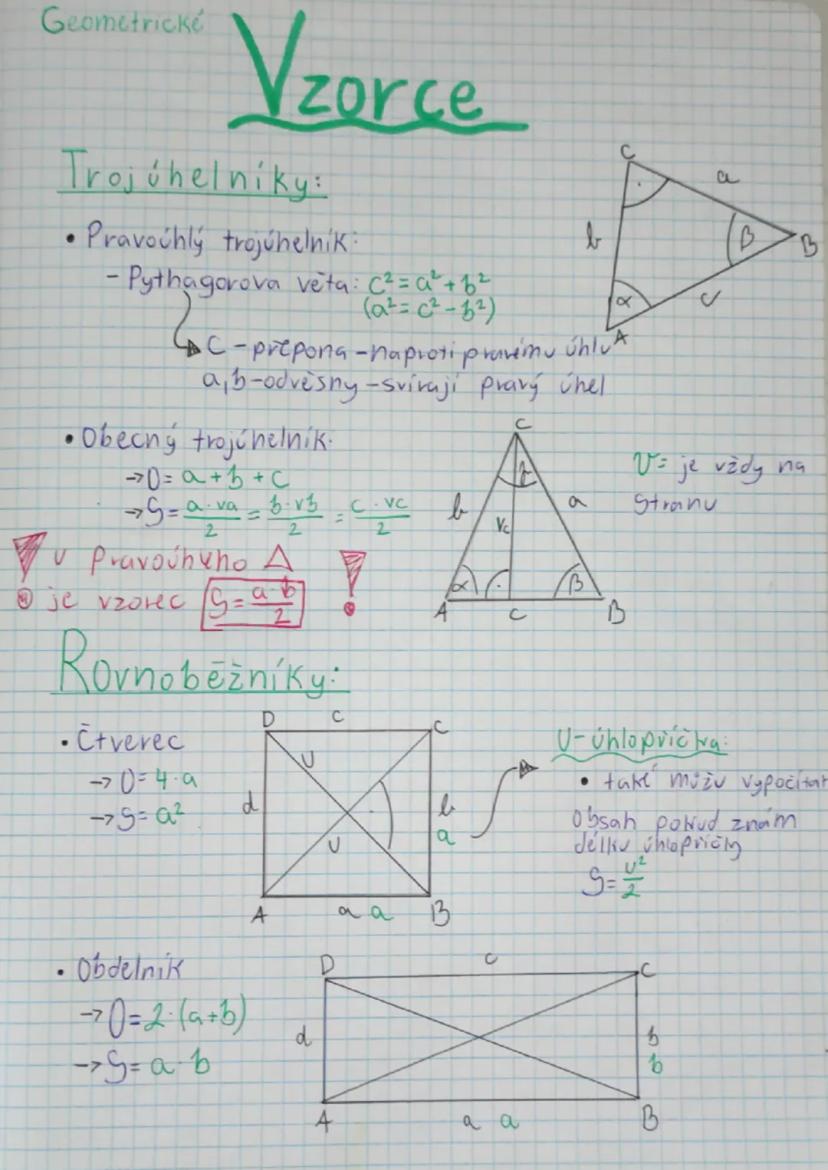
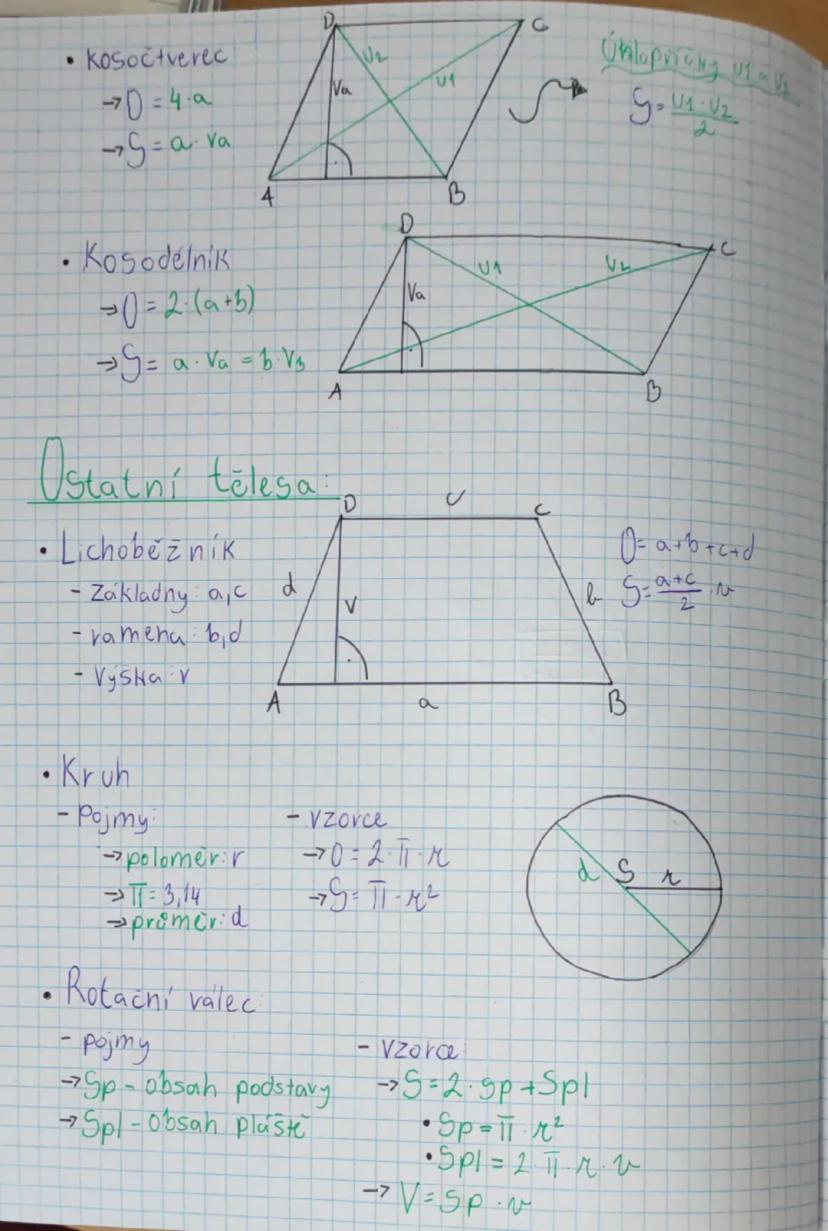
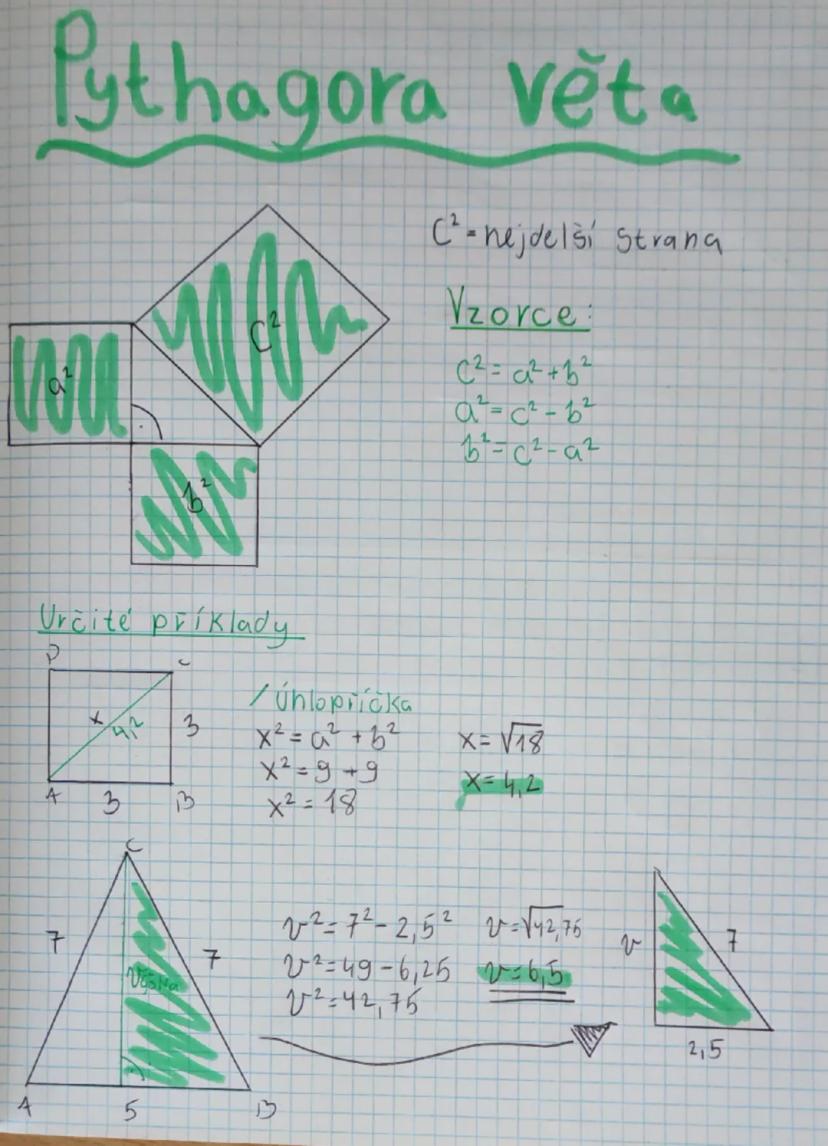
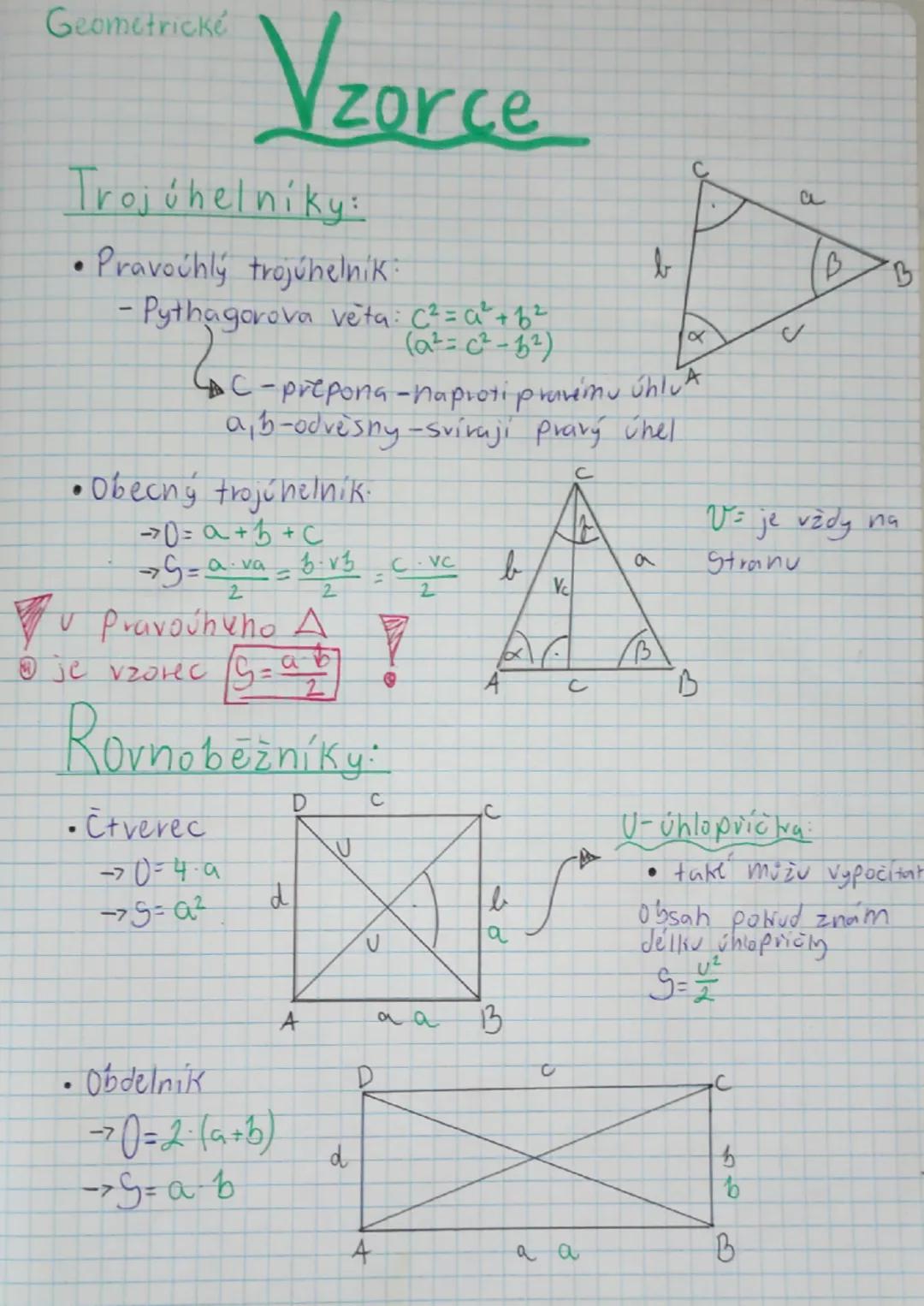
Krychle je jednoduchá - má povrch S = 6a² a objem V = a³, kde a je délka hrany. U kvádru se strany označují a, b, c a platí S = 2 · $ab + bc + ca$ a V = a · b · c.

Pro kouli o poloměru r platí povrch S = 4πr² a objem V = (4/3)πr³. Vzorce si nemusíš pamatovat přesně, stačí vědět, že obsahují π a mocniny poloměru.

Rotační válec má objem V = πr² · v a povrch S = 2πr² + 2πrv, kde r je poloměr podstavy a v je výška. Zkráceně: S = 2S_p + S_pl, kde S_p je obsah podstavy a S_pl je obsah pláště.

✨ Představ si tělesa prostorově - krychle je jako kostka, válec jako plechovka a koule jako míč. Pomůže ti to lépe pochopit jejich vlastnosti!

Rotační kužel má povrch S = πr² + πrs, kde s je délka strany (tzv. strana pláště) a objem V = (1/3)πr²v, kde v je výška. A nakonec hranol má povrch S = 2S_p + S_pl a objem V = S_p · v.

Pythagorova věta v praxi

Pythagorova věta je jeden z nejdůležitějších vztahů v geometrii. V pravoúhlém trojúhelníku platí: c² = a² + b², kde c je přepona (nejdelší strana) a a, b jsou odvěsny.

Z tohoto vzorce si můžeš vyjádřit libovolnou stranu, když znáš ty ostatní:

• c = √$a² + b²$
• a = √$c² - b²$
• b = √$c² - a²$

Pythagorova věta se hodí třeba při výpočtu úhlopříčky obdélníku. Pokud máš obdélník se stranami 3 a 3, úhlopříčka x bude: x² = 3² + 3² = 18, takže x = √18 ≈ 4,2.

🌟 Když dostaneš pod odmocninou číslo, které není druhou mocninou, nemusíš výsledek vždy převádět na desetinné číslo. V některých případech stačí nechat výsledek ve tvaru odmocniny, např. √18.

Tuto větu využiješ i pro složitější výpočty - třeba když potřebuješ zjistit vzdálenosti v prostoru nebo vypočítat délky stran v různých geometrických útvarech.